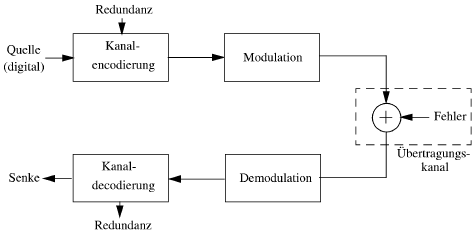
3 Fehlerkorrektur

3.1 Warum Fehlerkorrektur

Da dem digitalen Signal Redundanz und Irrelevanz durch Quellencodierungsverfahren entzogen werden, um die Datenrate klein zu halten, wird das Signal anfälliger gegen Bitfehler, die durch Störungen (z.B. Rauschen) auf dem Übertragungskanal entstehen. Damit diese Fehler nach der Übertragung wieder korrigiert werden können, werden zuvor Korrekturbits hinzugefügt, die jedoch keine eigentliche Information tragen, sondern lediglich dem Fehlerschutz dienen. Natürlich dürfen die hinzugefügten Daten in unserem Fall mengenmässig nicht grösser sein als die zuvor entfernten, was effektive Codierverfahren der Fehlerkorrektur erfordert.

Bild 3.1 Übertragung mit Fehlerschutzcodierung

3.1.1 Fehlerarten

Je nach Art der Störung, die die Fehler bei der Übertragung verursachen, gibt es verschiedene Bitfehlermuster. Wird nur ein einzelnes Bit verfälscht, spricht man von einem Bitfehler. Ein n Bit Burstfehler ist definiert durch einen Block der Länge n Bit, bei dem mindestens das erste und das letzte Bit falsch sind. Ein Symbolfehler bezeichnet ein verfälschtes Symbol der Länge l (oft ist l=8, ein Symbol=1 Byte), innerhalb dessen bis zu l Bitfehler beliebiger Zusammensetzung auftreten dürfen.

3.1.2 Codearten

Zwei wichtige Codearten sind der Blockcode und der Faltungscode. Beim Blockcode werden die Eingangsdaten in Blocks der Länge m aufgeteilt (m = Anzahl der Symbole) und nach jedem Block werden k Redundanzbits hinzugefügt, somit beträgt die neue Blocklänge n=m+k Bit. Die Coderate R ist definiert als Verhältnis der Informationsbits m zu Gesamtblocklänge n. Blockcodes eignen sich somit zur Korrektur von Symbolfehlern.

Der Faltungscode hingegen "verschmiert" die Eingangsdaten über mehrere Ausgangsbits. Die Eingangsdaten werden dazu in ein Schieberegister eingelesen, und die Ausgangsdaten durch die Kombination verschiedener Abgriffe am Register erzeugt. Die Coderate R ist hier definiert als Quotient der m auf einmal eingelesenen Bits zu den n auf einmal ausgelesenen Bits. Durch diese Art der Codierung sind Faltungscodes dazu geeignet, einzelne Bitfehler zu korrigieren.

3.1.3 Die Bitfehlerrate

Bei einem digitalen Signal wird die Qualität nicht durch den Signal-Rauschabstand angegeben, sondern durch die Bitfehlerrate. Sie ist definiert als Verhältnis der Häufigkeit fehlerhaft empfangener Bits zur Gesamtanzahl empfangener Bits.

3.2 Fehlerkorrekturverfahren

Nachfolgend werden verschiedene Fehlerkorrekturverfahren vorgestellt, die im Zusammenhang mit dem DVB-Standard eine wichtige Rolle für die Übertragung der digitalen Fernsehsignale spielen (siehe auch Kapitel 7).

3.2.1 Der Reed-Solomon Code

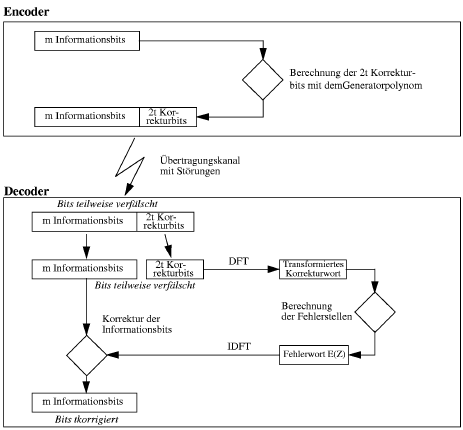
Reed-Solomon Codes sind symbolorientierte Blockcodes, die sowohl das defekte Symbol im Block erkennen als auch korrigieren können. Die Berechnungen für En- und Decodierung finden in einem abgeschlossenen Zahlenraum statt. Im Falle eines Binärcodes mit der Symbollänge l=8 Bit enthält dieser q=2 hoch l=256 Elemente. Solch einen abgeschlossenen Zahlenraum nennt man Galois-Feld GF(q). Auf die genaue Definition des Galois-Feldes soll hier nicht näher eingegangen werden, für eine nähere Betrachtung siehe [1] und [28].
Sollen mit einem Reed-Solomon Code t verfälschte Symbole in einem Block mit n Symbolen korrigiert werden, müssen 2t Korrektursymbole angehängt werden. Die Reed-Solomon Encodierung ist sowohl im Zeit- als auch im Frequenzbereich möglich. Wir wollen hier genauer auf das Prinzip des komplexen Algorithmus zur En- und Decodierung nach dem DVB-Standard eingehen:
Die Informationssymbole werden im Encoder so angeordnet, dass sie in den ersten m Stellen des zu übertragenden Codewortes stehen. Dieses Codewort wird nun durch ein spezielles Codewort geteilt, das Generatorpolynom. Dieses Polynom hat die Eigenschaft, dass seine Nullstellen 2t aufeinanderfolgende Nullen im Spektrum zur Folge haben. Die k Stellen des Ergebnisses dieser Modulodivision werden hinter die m Stellen im zu übertragenden Codewort gehängt. Dieses derart zusammengesetzte Wort c(x) mit n=m+k Stellen besitzt nun die Eigenschaft, dass sein Spektrum die gleichen 2t hintereinanderfolgende Nullstellen besitzt. Wenn das Codewort nach der Übertragung diese Eigenschaft verloren hat, weiss der Decoder, dass es verfälscht worden ist. Er kann nun mit Hilfe verschiedener Algorithmen und Rechenoperationen im Frequenzbereich ein Fehlercodewort E(Z) erzeugen und somit wieder die ursprüngliche Information R(Z)=C(Z)-E(Z) zurückgewinnen. Nach der Rücktransformation in den Zeitbereich steht am Ausgang die ursprüngliche Information r(x) zur Verfügung.

Bild 3.2 Reed-Solomon Codewörter im Zeit- und Frequenzbereich

Für ein mathematisch anschauliches Beispiel einer Reed-Solomon En- und Decodierung im Frequenzbereich siehe [1].
Ein Reed-Solomon Code mit m Informationsbytes (hier: 1 Symbol = 1 Byte) und k Korrekturbytes wird ein RS(m+k,m) Code genannt. Ein derartiger Code kann maximal k/2 falsche Symbole pro Codewort korrigieren und k erkennen.

Bild 3.3 Restbitfehlerwahrscheinlichkeit verschiedener RS- Codes

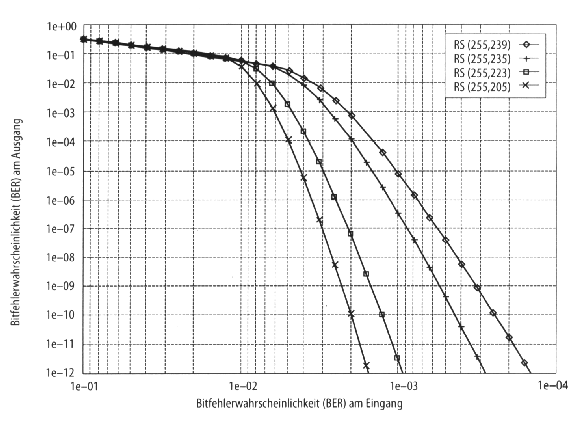
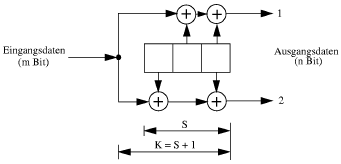
Obwohl die Reed-Solomon Codes symbolorientierte Codes sind, geht man bei der Analyse ihrer Leistungsfähigkeit von Bitfehlern aus. Unter der Annahme der Gleichverteilung der Bitfehler, lässt sich eine Aussage über die Symbolfehlerrate treffen, mit deren Hilfe die Leistungsfähigkeit eines Reed-Solomon Codes analysiert werden kann (Bild 3.3).

3.2.2 Faltungscodes

Faltungscodes sind Binärcodes, bei denen die Eingangsbits über mehrere Ausgangsbits "verschmiert" werden. Bei der Encodierung werden die Eingangsdaten in ein Schieberegister gelesen und die Ausgangsdaten durch Kombinationen von Abgriffen ermittelt (meistens sind es Exor-Verknüpfungen).

3.2.2.1 Der Encoder

Bild 3.4 Beispielaufbau eines Faltungsencoders

Charakteristische Daten des Beispielencoders:

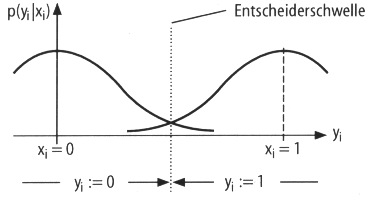
3.2.2.2 Der Decoder

Da bei der Übertragung durch einen realen Kanal das Signal üblicherweise gestört wird, sind am Empfänger die Amplituden der digitalen Signale nicht mehr diskret, sondern über den gesamten Bereich verstreut. Die Werte lassen sich somit nur noch statistisch beschreiben. Um aus dem verfälschten Signal wieder die ursprünglichen diskreten Werte zu erhalten, wird im Empfänger ein Viterbi-Decoder mit vorgeschalteter Hard- oder Softdecision eingesetzt. Dieser errechnet aus den Empfangsdaten aufgrund der grössten Wahrscheinlichkeit die Originaldaten. Wird Harddecision eingesetzt, liegt die Entscheidungsschwelle in der Mitte zwischen den Amplitudenwerten, die den Zuständen 0 und 1 entsprechen:

Bild 3.5 Wahrscheinlichkeitsdichteverlauf des Empfangssignals und Entscheidungsschwelle bei Harddecision

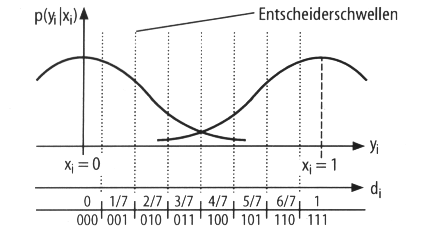
Bei Softdecision hingegen verwendet man mehrere Schwellen, was zu einer genaueren Abschätzung führt, aber natürlich auch mehr Aufwand bedeutet. Bei einem Viterbi-Decoder mit Softdecision (sieben Schwellen und somit acht Bereiche codiert mit 3 Bit) liegt der typische Codierungsgewinn gegenüber einer Harddecision bei 2 dB (siehe dazu auch Bild 6.7):

Bild 3.6 Quantisierung des Eingangssignals durch mehrere Entscheidungsschwellen bei Softdecision

3.2.2.3 Punktierung von Faltungscodes

Um die Coderate von Faltungscodern zu erhöhen (im Beispiel ist R = 1/2), gibt es die Möglichkeit, im Ausgangsstrom wieder Bits zu entfernen. Dabei verringert sich sowohl die Redundanz und somit auch die Menge der zu übertragenden Daten als auch die Korrekturfähigkeit des Codes. Dieser Vorgang wird Punktierung genannt. Streicht man z.B. jedes dritte Bit am Ausgang, steigt die Coderate auf R = 3/4.

3.2.2.4 Leistungsfähigkeit von Faltungscodes

Bild 7.6 (Kapitel 7, S. 53) zeigt die Restbitfehlerwahrscheinlichkeit von Faltungscodes mit R = 1/2 bei verschiedenen Eb/N0. Dabei ist Eb/N0 definiert als Energie Eb, die pro Bit übertragen wird, bezogen auf die Rauschleistungsdichte N0 des dem Signal auf dem übertragungskanal überlagerten weissen Gaussschen Rauschen. Es wird dabei eine Übertragung mit QPSK-Modulation angenommen, und K bezeichnet die Beeinflussungslänge des verwendeten Codes.

3.2.2.5 Verkettung von Codes

Eine Möglichkeit, um die Effizienz von Codes zu erhöhen, liegt darin, verschiedene Codes miteinander zu verketten. Der erste Code (mit der Coderate R1) wird äusserer Code, der zweite (mit der Coderate R2) innerer Code genannt. Bei einer zu übertragenden Coderate Ru ergibt sich die Gesamtdatenrate zu

Bild 3.7 Verkettung von Codes mit den zugehörigen Datenraten

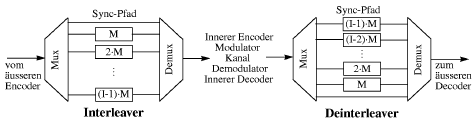
Wird z.B. als äusserer Code ein Blockcode und als innerer Code ein Faltungscode gewählt, so kann der innere Code einzelne Bitfehler korrigieren und der äussere kleinere Burstfehler. Um auch längere Burstfehler korrigieren zu können, schaltet man zwischen die beiden Coder einen Interleaver. Dieser fügt keine neuen, redundanten Daten hinzu, sondern er sortiert die Daten derart um, dass zuvor nebeneinanderliegende Bits nachher um die Interleavingtiefe I auseinanderliegen.

3.2.2.6 Der Interleaver

Bild 3.8 Prinzip der Funktionsweise eines Faltungsinterleavers

Der Interleaver liest die Daten zeilenweise in eine Speichermatrix ein und spaltenweise wieder aus. Die Anzahl der Spalten gibt somit die Interleavingtiefe vor. Die Verzögerung durch das Interleaving ist durch die Anzahl Zeilen M der Matrix festgelegt. Mit dieser Methode werden falsche Bits längerer Burstfehler auseinandergerissen und können so Bitweise vom inneren Code korrigiert werden. Ein Nachteil besteht darin, dass periodische Bitfehler möglicherweise durch Interleaving aneinandergereiht werden und somit nach dem Interleaver längere Burstfehler entstehen, die nicht mehr korrigiert werden können.