|
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
2 Datenreduktion nach der MPEG2 - NormÜbertragungskanäle und Speichermedien haben nur beschränkte Kapazitäten, was aus technischen und ökonomischen Gründen eine Datenreduktion unabdingbar macht. Ein 4:2:0 Videosignal hat beispielsweise eine Datenrate von 124.5 Mbit/s während ein 33 MHz Satellitenkanal bei einer Bandbreitenausnutzung von 1.57 bit/s pro Hz lediglich 52 Mbit/s übertragen kann.
2.1 Grundlagen der DatenreduktionEin Ziel der Quellencodierung besteht darin, die Datenreduktion so durchzuführen, dass diese für den Beobachter subjektiv nicht oder kaum wahrnehmbar ist. Dies wird durch Ausnutzung gewisser psychovisueller und -akustischer Effekte erreicht (Irrelevanzreduktion). In der Optik sind das unter anderem folgende: Mach-Effekt: Kontrastübergänge an Kanten werden verstärkt wahrgenommen Oblique-Effekt: In der Natur sind überwiegend horizontale und vertikale Strukturen anzutreffen. Der Mensch ist deshalb bei der Orientierung weniger auf diagonale Strukturen angewiesen. Letztere können also bei der Kodierung rudimentär behandelt werden. Flächenintegration: Je grösser eine einfarbige Fläche ist, desto genauer können Farb- und Helligkeitswerte aufgelöst werden - das Auge kann "integrieren". Der Coder muss also grosse Flächen (kleine Frequenzen im Ortsraum) genauer quantisieren als kleine. Es werden zwei Reduktionsansätze unterschieden und im folgenden beschrieben: 2.1.1 Redundanzreduktion und Entropie
Ein Signal enthält redundante Information, wenn diese durch Kenntnisse der Statistik der Nachrichtenquelle vorhersagbar ist. Wenn etwa zwei benachbarte Bildpunkte untereinander korrelieren, spricht man von räumlicher Redundanz, bei korrelierenden Farbflächen oder Frequenzbändern von spektraler Redundanz. Die ähnlichkeit zweier aufeinander folgenden Bilder wird als zeitliche Redundanz bezeichnet. P(x)X: diskrete Wahrscheinlichkeitsverteilung b: Basis des Kodieralphabets; binär: b = 2 Die Entropie wird maximal, wenn X gleichverteilt ist. Weisen jedoch die Signalzustände verschiedene Wahrscheinlichkeiten auf, sind Informationsgehalt und Entropie kleiner. Ein Extrembeispiel: Der Signalwert xihabe die Wahrscheinlichkeit 1, alle restlichen die Wahrscheinlichkeit 0. Damit ist der Informationsgehalt gleich Null und eine übertragung erübrigt sich. Wenn also P(x)Xstark schwankt, was bei Videosignalen der Fall ist, kann das m-wertige Signal mit weniger als den ursprünglichen n = ld(m) Bits übertragen werden. Die Entropie H(x) ist dabei eine untere Schranke für die bestenfalls erreichbare durchschnittliche Codewortlänge. Der Huffman Algorithmus kommt dieser Schranke am nächsten und liefert Codewortlängen, deren Erwartungswert der folgenden Ungleichung genügt: Das Ziel der Redundanzreduktion ist, mittels einer Transformation die Datenrate der Quelle zu verringern, so dass eine effiziente Entropiekodierung möglich wird. 2.1.2 Irrelevanzreduktion
Die Signalanteile, die das Auge bzw. das Gehör auf Grund des beschränkten Auflösungsvermögens nicht aufnehmen kann, sind irrelevant und brauchen bei der Kodierung nicht berücksichtigt zu werden, sie sind allerdings durch den Decoder nicht wiederherstellbar. Auch hier trifft man auf räumliche, spektrale und zeitliche Irrelevanz. 2.2 Video - Quellenkodierung nach MPEG2
Während MPEG1 im Multimediabereich mit dem Speichermedium CD bei geringen Datenraten von 1.15 Mbit/s seine Anwendung findet, dient die Erweiterung MPEG2 der übertragung von Fernsehsignalen im Zeilensprungverfahren. Das "Main Profile at Main Level" sieht Datenraten von bis zu 15 Mbit/s vor, wobei schon 6 Mbit/s mit der Qualität der PAL Norm vergleichbar und 9 Mbit/s subjektiv kaum vom Original (Studioqualität, RGB) zu unterscheiden ist (Visuelle Transparenz). Wir werden uns im folgenden auf das für DVB vorgesehene 4:2:0 Format beschränken, weitere mögliche Eingangsformate sind in Tabelle 4 aufgelistet.
2.2.1 Video VorverarbeitungDie analogen RGB Komponenten werden nach der AD-Wandlung durch eine lineare Matrixtransformation in den YC1C2-Farbraum konvertiert, was die spektrale Redundanz verringert. Ferner werden so die hohen Frequenzen in der Luminanzkomponente konzentriert, weil das Auge hohe Chrominanzfrequenzen nicht so gut auflösen kann. Nach einer Tiefpassfilterung (wegen Aliasing) werden die Chrominanzkomponenten um den Faktor 2 horizontal und vertikal unterabgetastet. Die Organisation der so entstandenen digitalen 4:2:0 Bilddaten wird im nächsten Abschnitt beschrieben. 2.2.2 Datenorganisation - LayerstrukturMPEG organisiert die Videodaten in sechs Layerhierarchien (siehe Tabelle 2). Die oberste Schicht, der Sequence-Layer, ermöglicht den Kontextzugriff auf eine Bildsequenz. In seinem Header stehen u.a. Informationen zum Bildformat und Rahmenparameter für den Decoder.
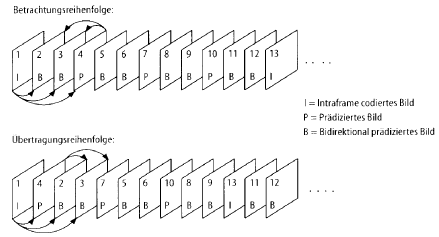
Tabelle 2 MPEG Layerhierarchien Bild 2.3 zeigt den Aufbau einer Bildgruppe (Group of Pictures) im GOP-Layer. Er erlaubt den (Wieder-) Einstieg in den Dekodierprozess innerhalb maximal einer halben Sekunde nach einem Programmwechsel oder einer Störung mit Bildausfall. Es werden je nach Kodierungsart drei verschiedene Bildtypen unterschieden: - I (Intra) - Bild: Codierung nur auf Grund eigener Bilddaten- P (Prediction) - Bild: Codierung unidirektional aus vorhergehenden I- oder P-Bild - B (Bidirectional) - Bild: Codierung bidirektional aus einrahmenden P- oder I-Bildern
I-Bilder werden ohne Zuhilfenahme von vorhergehenden Bildern codiert, weil andernfalls der Einstieg in den Dekodierprozess nicht möglich wäre. P-Bilder entstehen durch Bewegungsschätzung aus dem letzten I- oder P-Bild, während die Prädiktion von B-Bildern auch das folgende I- oder P- Bild berücksichtigt. Damit lässt sich die Codiereffizienz nochmals deutlich steigern, was aber zur Folge hat, dass die Bilder zeitlich umsortiert werden müssen (Bild 2.3). Coder und Decoder besitzen aus diesem Grunde Bildspeicher. Informationen zur Bildcodierung stehen im Picture Layer Header. 2.2.3 Differenzcodierung mit Bewegungsschätzung
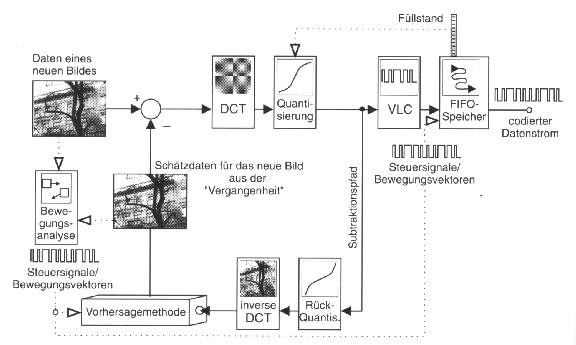
Zwei zeitlich aufeinanderfolgende Bilder sind - Szenenwechsel ausgenommen - sehr ähnlich und beinhalten zeitliche Redundanz. Wird jedoch nur das Differenzbild codiert, fällt die Entropie wesentlich günstiger aus. Weitere Verbesserungen lassen sich erzielen, wenn nicht das Differenzbild, sondern das bewegungskompensierte Residuum und die entsprechenden Bewegungsvektoren codiert werden: Es wird macroblockweise analysiert, in welche Richtung sich der Inhalt eines Blockes verschiebt. Der Decoder erhält diese Information in Form von Bewegungsvektoren. Zur Bildrekonstruktion werden die Blöcke des alten Bildes gemäss der Vektoren verschoben und das Residuum addiert. Es gibt verschiedene Verfahren zur Bewegungsschätzung. Beim Block-Matching Verfahren werden die Macroblöcke in einem definierten Suchbereich verschoben und ein Korrelationsfaktor bestimmt. 2.2.4 DCT - CodierungMit Hilfe der Diskreten Cosinustransformation kann dem Signal räumliche Redundanz und Irrelevanz entzogen werden. Die DCT ist wie folgt definiert, wobei bei einer 8x8 Blockgrösse N=8 gewählt wird:
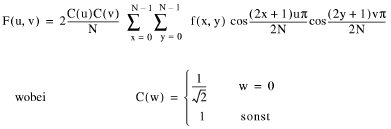 (2.3) (2.3)
Die Darstellung der Bilddaten durch DCT- Koeffizienten hat den Vorteil, dass sich die nur im Blockverbund erfassbare räumliche Redundanz (z.B Farbflächen) durch die Transformation verringert, weil sich die Signalenergie auf wenige Koeffizienten konzentriert. Dies sind die Koeffizienten kleiner Frequenzen und vor allem die Grundfrequenz.
Tabelle 3 MPEG2 Quantisierungstabelle 2.2.5 DatenratenkontrolleMPEG2 benutzt bei der übertragung konstante Datenraten. Bei sehr lebhaften Bildinhalten und eventuellem Versagen der Bewegungsschätzung droht ein überlaufen des Ausgangspuffers. Zur Regelung der Datenrate wird der Quantisierer beeinflusst, indem je Macroblock ein globaler Quantisierungsfaktor eingeführt wird, der auf Werte zwischen 1 und 31 eingestellt werden kann. Die DCT Quantisierung wird also insgesamt wie folgt realisiert:
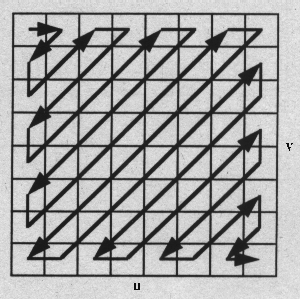
2.2.6 Lauflängen- und HuffmancodierungBei der Quantisierung der DCT Koeffizienten, werden die meisten Werte - bis auf wenige in der Umgebung des DC Anteils - zu Null. Durch ein Auslesen nach der Zick-Zack-Methode werden die Nullen zu einer Nullfolge zusammengelegt (Bild 2.5).
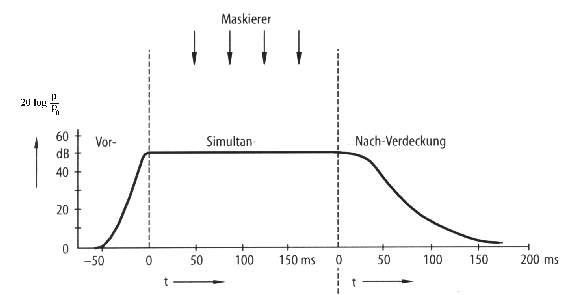
Die Lauflängencodierung fasst jeweils die Anzahl der Nullen und den ersten nächsten von Null verschiedenen Koeffizienten zu einem Zahlenpaar zusammen. Anschliessend werden diese Paare huffmancodiert, indem dessen Auftrittswahrscheinlichkeiten bei der Vergabe der Codewortlängen berücksichtigt wird. 2.3 Audio-Quellencodierung nach MPEG2Audiosignale enthalten - Sprachsignale ausgenommen - nur wenig Redundanz, weshalb bei der Audiodatenreduktion nur Irrelevanzen berücksichtigt werden können. Man macht sich hierbei die beschränkte spektrale und zeitliche Auflösung des Gehörs zu Nutze. Diese wird durch ein psychoakustisches Modell beschrieben, das dem Encoder zugrunde liegt. Es ist zu bemerken, dass das Gehör feiner als das Auge auflösen kann und Störungen eher wahrnimmt. 2.3.1 Psychoakustische GrundlagenSchallpegel, die unter der Ruhehörschwelle liegen werden nicht wahrgenommen. Diese Schwelle ist frequenzabhängig und wird in Bild 2.7 - normiert auf den Pegel bei 2 kHz - dargestellt. Ein lauter Ton hebt diese Schwelle in seiner spektralen Umgebung an, dass heisst ein etwas leiserer Ton ähnlicher Frequenz ist nicht mehr hörbar. Dies wird als Verdeckungseffekt bezeichnet. Dabei tritt die Verdeckung nicht nur simultan, sondern auch vor und nach dem maskierenden Ton auf (Bild 2.6).
2.3.2 Codierverfahren
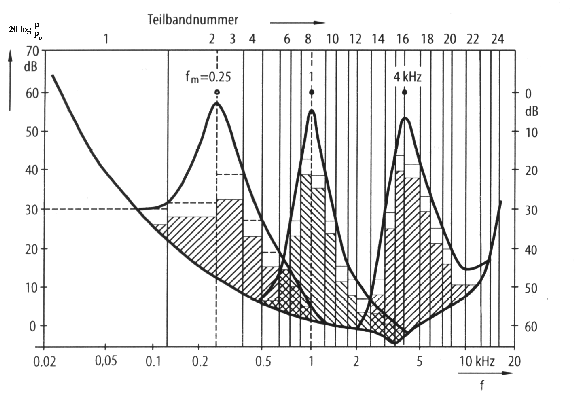
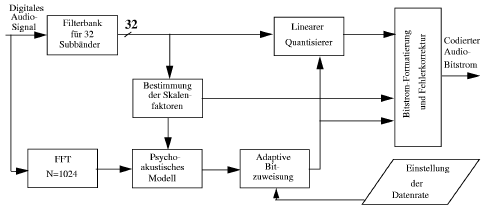
Der MPEG-Coder stützt sich bei der Datenreduktion auf den Verdeckungseffekt, indem er gerade so fein quantisiert, dass das resultierende Quantisierungsrauschen, das bei hinreichenden kleinen Stufen als gleichverteilt und weiss angesehen werden kann, unter der Maskierungsschwelle bleibt und somit nicht hörbar ist (Noiseshaping). Dazu wird das Audiosignal einer Filterbank zugeführt, die dieses in 32 Frequenzbänder aufteilt. In jedem dieser Bänder wird mittels einer FFT nach maskierenden Tönen gesucht, deren tonalen Eigenschaften bestimmt und daraus die Maskierungsschwellen ermittelt. Die Feinheit der Quantisierung wird nun in einem iterativen Prozess so geregelt, dass der Abstand des Quantisierungsrauschens zur Maskierungsschwelle bei fixer Ausgansdatenrate möglichst gross wird. Bild 2.7 zeigt die Maskierungsschwellen in Anwesenheit dreier Maskiertöne und das verdeckte Quantisierungsrauschen.
2.4 Gracefull Degradation und SkalierbarkeitBei digitalen übertragungsverfahren herrscht das "Alles oder Nichts" Prinzip. überschreitet die Bitfehlerrate eine gewisse Schwelle, versagt die Fehlerkorrektur und der Bildschirm bleibt schwarz. Dies kann bei schwachen Satelliten, kleinen Empfangsantennen und schlechter Witterung zu einem ständigen Wechsel zwischen Empfang und Ausfall führen. Bei Analogen Systemen dagegen wird das Bild in so einem Fall zunehmend schlechter und fällt erst bei sehr kleinen SNRs aus (Gracefull Degradation). Das Konzept der Skalierbarkeit soll ein ähnliches Ausfallverhalten bei der digitalen übertragung bewirken. Dazu wird der Basisinformation des Signals eine höhere Priorität beim Fehlerschutz eingeräumt. Es werden folgende Skalierungsarten unterschieden: Die SNR Scalability teilt den höherwertigen Bits eine bessere Fehlerkorrektur zu. Das hat zur Folge, dass bei schlechtem Empfang zuerst die niederwertigen Bits ausfallen, was sich als rauschartige Störung bemerkbar macht. Bei der Spatial Scalability erhält ein durch Unterabtastung mit dem Faktor 2 räumlich schlechter aufgelöstes Bild eine höhere Priorität (Base Layer), das bei normalem Empfang durch einen Enhancement Layer verfeinert wird. Ganz ähnlich skaliert die Temporal Scalability mit der Bildwiederholfrequenz die zeitliche Auflösung. Der MPEG2 Standard definiert verschiedene Levels und Profiles, die sich in den angewandten Algorithmen und Auflösungen unterscheiden. Sie sind in Tabelle 4 zusammengefasst. DVB hat sich auf das "Main Profile at Main Level" festgelegt und verzichtet somit auf das Prinzip der Skalierbarkeit.
Tabelle 4 Profiles und Levels bei MPEG2 Die Werte in den Klammern beziehen sich auf Base und Enhancement-LayerEs ist noch zu erwähnen, dass MPEG nur den Syntax und die Semantik des Bitstromes und die Kompressionsalgorithmen beschreibt, wobei keine spezielle Anwendung bevorzugt wurde. Damit ist einerseits die Kompatibilität und ein breiter Anwendungsbereich gesichert, anderseits ist die konkrete Realisierung dem Einzelnen überlassen, so dass zukünftigen Verbesserungen nichts im Wege steht. |