 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Psychovisuelle GrundlagenEinleitungIn fast allen Systemen, die eine Art von Bildcodierung mit Datenreduktion verwenden, ist der schlussendliche Empfänger des wiederhergestellten Bildsignals (Videosignal oder Stillbild) das menschliche Auge. Es sollte daher von vorherein klar sein, dass Anstrengungen unternommen werden müssen, ein Modell der Arbeitsweise des menschlichen Sehens (Human Visual System, HVS) in die Verarbeitungskette miteinzubeziehen. Denn nur so kann sichergestellt werden, dass a) beim Codiervorgang die Bits vorzugsweise denjenigen Teilen im Ausgangssignal zugewiesen werden, die denjenigen Strukturen im Bild entsprechen, auf welche das Auge am empfindlichsten reagiert, und dass b) ein damit verbundenes numerisches Qualitätsmass geschaffen werden kann, das die umfassenden subjektiven Tests mit Versuchspersonen als Mittel für den Vergleich der Wirksamkeit mehrerer Algorithmen erübrigen würde [8], [18]. Eigenschaften des AugesVor der Entwicklung eines Modells für ein HVS, ist es notwendig, die physikalischen Eigenschaften des Auges und die Abläufe beim Wahrnehmen von Bildern und Szenen zu betrachten. Die hier dargestellte Übersicht ist kurz gehalten, detailliertere Ausführungen finden sich in [19], [20], [21]. Für den Menschen sichtbares Licht umfasst ungefähr den Wellenlängenbereich von 400 nm (violett) bis 700 nm (rot) und wird durch die Linse (ihre Apertur ist durch die Iris einstellbar zwischen 2 und 8 mm) auf die lichtempfindliche und ca. 17 mm entfernte Netzhaut abgebildet. Die auftreffende Lichtintensität wird mittels einer photochemischen Reaktion durch zwei Arten von Sensoren, Stäbchen und Zapfen, ermittelt. Die Stäbchen besitzen die größere Empfindlichkeit, unterscheiden jedoch keine Farben. Dafür arbeiten sie noch bei sehr wenig Licht (skoptisches Sehen). Die Zapfen sind zuständig für stärkere Intensitäten (photopisches Sehen), feine Auflösungen und das Farbensehen. Für letztgenannten Vorgang sind sie in drei verschiedene Arten aufgeteilt, wobei jede ein Absorptionsmaximum an einer anderen Stelle innerhalb des sichtbaren Spektrums besitzt ( bei rot-orange, grün und blau-violett). Zusammen erlaubt das System mit zweierlei Sensoren das Sehen über einen Intensitätsbereich von 11 Grössenordnungen (10-6 bis 105 cd/m2). Das bedeutet, dass innerhalb der verschiedenen Stufen des Wahrnehmungsprozesses eine Anpassung an die Hintergrundsintensität in einem grossen Bereich stattfindet (Bild 5.1).
 Die beiden Rezeptortypen sind auf der Netzhaut nicht gleichmässig angeordnet. Die insgesamt ca. 6·106 Zapfen konzentrieren sich im sogenannten gelben Fleck, einem kleinen Teil der Netzhaut mit ca. 0,5 Millimeter Durchmesser im Bereich rund um die optischen Achse der Linse (Fovea), in dem die Flächendichte ca. 150'000 Zellen pro mm2 beträgt . Die Fovea ist der Ort der maximalen Sehschärfe und bildet ein Sehfeld in einem Winkel von etwa 1.5 Grad, innerhalb dessen der Beobachter seine Umgebung mit maximaler Auflösung wahrnimmt. Die Dichte der Zapfen nimmt nach aussen hin ab, wohingegen die der Stäbchen zunimmt (im gelben Fleck befinden sich ausschliesslich Zapfen). Die maximale Stäbchendichte von ebenfalls ca. 150'000 pro mm2 befindet sich in einem Winkel von 20 Grad bezüglich der Sehachse, am Rand des Sehfelds (70 - 80 Grad) ist sie nur noch halb so gross [39]. Weil das Netzwerk von Sehzellenverbindungen, Nervenzellen und optischen Nervenfasern zwischen den lichtempfindlichen Zellen und der Linse liegt, ergibt sich auf der Netzhaut ein sogenannter blinder Fleck", in dem sich weder Stäbchen noch Zapfen befinden, sondern wo der Strang der Sehnerven das Auge verlässt. Dieser enthält viel weniger Nervenfasern (ungefähr 8·l05) als Stäbchen und Zapfen vorhanden sind. Denn obwohl in der Fovea jeder Zapfen mit einem eigenen Nerv verbunden ist, sind an der Sichtperipherie 100 oder mehr Stäbchen mit einer einzelnen Nervenzelle verkoppelt. Somit sind unterschiedlich viele Rezeptoren je nach Region der Netzhaut miteinander auf verschiedene Arten verschaltet, bevor die Impulse auf den abgehenden Sehnerv übertragen werden. Diese komplizierte Vernetzung bildet die Grundlage für die Verarbeitung der visuellen Informationen. Die Übermittlung dieser Informationen entlang des Sehnervenstrangs findet in Form von Impulsfolgen (Pulsdichtemodulation) mit einer Maximalrate von mehreren hundert Impulsen pro Sekunde statt, deren Abstand voneinander von der jeweiligen optischen Reizstärke abhängt. Jedes sinnvolle HVS-Modell muss so viele Phänomene wie möglich berücksichtigen, die das Auge bei seiner täglichen Arbeit hervorruft. Auf diesem Gebiet ist bisher schon viel Arbeit geleistet worden, meistens jedoch unter Laborbedingungen und mit dem Ziel, verschiedene Wahrnehmungseffekte getrennt voneinander zu definieren und zu erklären. Grundsätzlich gibt es vier Dimensionen", in denen das Auge arbeitet, die in diesem Zusammenhang von Bedeutung sind, d. h. wie es sich als Funktion der unabhängigen Variablen (a) Intensität, (b) Variation der örtlichen Strukturen, (c) Variation der zeitlichen Strukturen und (d) Farbe verhält. Wenn man die Antworten auf diese Abhängigkeitsfragen kennen würde, wäre man in der Lage, ein vollständiges Modell des Sehsystems zu entwerfen. Unglücklicherweise sind, während einige Mechanismen in ihrem Ablauf innerhalb des HVS wissenschaftlich erklärt und gesichert sind, andere eher Mutmassungen unterworfen, und es gibt immer noch Meinungsverschiedenheiten über die angemessenen Erklärungsformen und Modelle. Es hat sich herausgestellt, dass die einzelnen Ergebnisse nicht voneinander trennbar sind in dem Sinn, dass ein bestimmter Reiz auch nur eine ganz klar vorherbestimmbare Auswirkung hat. Zum Beispiel sind die räumliche und zeitliche Auflösung miteinander verknüpft und dies trägt unvermeidlich zur Komplexität des Modells bei. Solange es sich noch um monochromatische Stillbilder handelt, vereinfacht sich die Angelegenheit zu einer Untersuchung der Augencharakteristik hinsichtlich der Intensität und der Variation der örtlichen Strukturen. Daraus lässt sich ein grundlegendes HVS-Modell ableiten, das sich nachträglich derart erweitern lässt, dass auch Farben und zeitliche Effekte berücksichtigt werden können. Amplitudenfrequenzgang des AugesWie wir bereits gesehen haben, ist das Auge in der Lage, einen enorm grossen Helligkeitsbereich (ca. 11 Zehnerpotenzen, siehe Bild 5.2) zu verarbeiten, von der Intensität des Sternenlichts bis zur Schmerzgrenze (Blendung).
 Da die Pupille ihren Durchmesser aber nur im Verhältnis 4:1 regeln kann, muss eine sehr weiträumige Anpassung an die durchschnittliche Szenenhelligkeit auf Rezeptorenebene der visuellen Wahrnehmung stattfinden, denn es ist weder möglich, die Erregerfrequenz für die Übertragungsimpulse auf den Nervenfasern um einen Faktor 109 - 1010 zu variieren [22], noch ist es in der Praxis notwendig. Für den täglichen Gebrauch ist ein viel geringerer Dynamikumfang ausreichend. Folglich ergeben Versuche, die den kleinsten wahrnehmbaren Unterschied zwischen dem angepeilten Sehbereich und einer kleinen umgebenden Fläche veranschaulichen sollen, Ergebnisse, die sehr stark von der Beschaffenheit des gesamten Hintergrunds abhängen (siehe Bild 5.3).
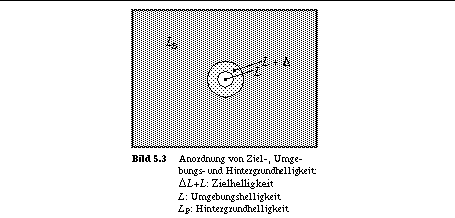 So lange LB = L ist, beträgt das gerade noch wahrnehmbare Kontrastverhhältnis L/L ungefähr 2% (Weber) in einem Bereich von L über vier Grössenordnungen des Amplitudenumfangs. Bei tieferen oder höheren Werten von L wird das Verhältnis grösser und das Auge wird folglich weniger empfindlich (Kurve [a], Bild 5.4). Bei konstant gehaltenem LB ist der Bereich, in dem L/L klein ist, bedeutend enger, wie in Kurve [b] zu sehen ist (Bild 5.4). Laut [23] beträgt der Dynamikumfang des Auges (bezüglich der Helligkeit) 2.2 logarithmische Einheiten und verschiedene andere Abschätzungen (vgl. [24]) bestätigen, dass bei gegebener Hintergrundhelligkeit (für die Adaption des Auges) die Anzahl der unterscheidbaren Helligkeitsstufen im Bereich von 150 bis 250 liegt.
Aus dem oben beschriebenen Experiment gewinnt man die wichtige Erkenntnis, dass die kleinste wahrnehmbare Helligkeitsdifferenz nicht als konstanter Wert erscheint, sondern abhängig vom konstanten Verhältnis
wobei L die Displayhelligkeit, E die elektrische Eingangsgrösse des Displays und Ortsfrequenzgang des AugesEs ist offensichtlich, dass feine Strukturen umso schlechter wahrgenommen werden können, je kleiner der Sehwinkel wird, unter dem sie betrachtet werden. Schliesslich können mit steigender Komplexität kleine Details gar nicht mehr separat aufgelöst werden. Das festigt die Behauptung, dass der Ortsfrequenzgang des Auges zu hohen Ortsfrequenzen (die Anzahl von vollständigen Schwingungen pro Grad eines sinusoidalen Helligkeitsmusters, die vom Auge unterschieden werden) hin auf vernachlässigbar kleine Werte abfällt. Versuche haben ebenfalls gezeigt, dass die Empfindlichkeit des Auges auf Bereiche konstanter Helligkeit (d. h. Ortsfrequenz = 0) klein ist. Damit der Mensch also überhaupt etwas sehen kann, muss die Anregung in einem beträchtlichen Frequenzbereich zwischen diesen beiden Grenzen liegen [23]. Es hat sich gezeigt, dass dieser Frequenzbereich nicht nur gut bestimmbar ist (obgleich er abhängig von absoluter Helligkeit und zeitlicher Veränderung ist), sondern es gibt auch experimentelle Belege dafür , dass das visuelle System den sichtbaren Bereich des Frequenzspektrums in Subbänder aufteilt und Ereignisse aufgrund der Ausgänge dieser Kanäle wahrnimmt. Dieser Umstand ist besonders aus der Sicht der Transformationscodierung interessant, da diese auf eine sehr ähnliche Weise arbeitet, indem die örtlichen Strukturen transformiert werden und dann ebenfalls in mehreren Subbändern, anstatt in einem einzigen, weiter verarbeitet und codiert werden . Untersuchungen über die Arbeitsweise dieser Mechanismen im HVS sollten deshalb dazu führen, dass die Koeffizienten eines solchen Systems derart verändert werden können, dass es sehr effizient wird. Betrachtet man den gesamten Frequenzgang des Auges, gibt es auch noch die Möglichkeit, die Kontrasttreue gegenüber der Auflösung abzuwägen. Denn in Bereichen mit feinen Details, die eine grosse Auflösung benötigen, ist das Auge toleranter gegenüber Abweichungen der absoluten Helligkeit (Bild 5.5).
 Es sollte an dieser Stelle erwähnt werden, dass das Verhalten des Auges im allgemeinen von der Arbeitsweise von Rezeptorgruppen geleitet wird. Innerhalb dieser gibt es einerseits Rezeptoren, die bei einer Erhöhung der Lichtstärke auch eine Erhöhung der Impulsgenerierung auslöst, die dann über die Nerven weiter transportiert werden. Beim anderen Typ bewirkt eine Erhöhung der Lichtstärke eine Verkleinerung der Impulsfrequenz (anregende und hemmende Typen) [19]. Diese beiden Rezeptortypen sind meistens auf zwei Arten gruppiert: entweder mittenstimulierend und umgebungshemmend oder umgekehrt (Bild 5.6).
 Desweiteren ist der Gesamtfrequenzgangt inhomogen, da die Verteilung solcher Rezeptorgruppen auf der Netzhaut ungleichmässig ist. Somit wird soger der Amplitudenfrequenzgang des Auges wie zuvor beschrieben von räumlichen Effekten verändert: einerseits vom Einfluss verschiedener Rezeptorgruppen, die auf Hintergrunds- und Umgebungshelligkeit reagieren, andererseits von der Abhängigkeit der Helligkeitsschwelle vom Sehbereich (siehe oben). Die Wahrnehmungseffekte, die beim Zusammenspiel verschiedener örtlicher Gegebenheiten entstehen, werden normalerweise mit den Erscheinungen des Simultankontrastes und den Mach-Bändern veranschaulicht. Beim Simultankontrast ändert sich die wahrgenommene Helligkeit eines anvisierten Bereichs , wenn die Helligkeit rund um den Bereich variiert wird, wobei dieser umso dunkler erscheint, je heller der Hintergrund wird. Die Verstärkung dieses Effekts hängt ausserdem von der vorhandenen Beleuchtung ab: Ist der Kontrast zwischen Bereich und Hintergrund klein, erhöht eine stärkere Gesamtbeleuchtung die wahrgenommene Bereichshelligkeit. Ist umgekehrt der Kontrast gross, erscheint der Bereich bei stärkerer Beleuchtung dunkler und es kann ein dazwischenliegender Kontrastbereich gefunden werden, bei der die Bereichshelligkeit konstant bleibt, auch wenn die Beleuchtung sich ändert [21]. Der zweite Effekt tritt bei einer abrupten Helligkeitsänderung auf und ist dafür verantwortlich, dass der Übergang schärfer erscheint, als er in Wirklichkeit ist. Somit verringert ein Bereich mit grosser konstanter Helligkeit die wahrgenomme Helligkeit eines angrenzenden Bereichs mit kleinerer (aber ebenfalls konstanter) Helligkeit. Das für diese beiden Effekte verantwortliche Phänomen ist als laterale Hemmung bekannt und kann in Bezug auf den Ortsfrequenzgang des Auges als Hochpassfilter modelliert werden, der eine deutlich reduzierte Empfindlichkeit auf Bereiche mit konstanter oder sich leicht ändernder Helligkeit besitzt und die gezielte Bestimmung von scharfen Kanten (z. B. den Umriss eines Objekts) erlaubt. In diesem Zusammenhang ist es wichtig, auf das Phänomen der örtlichen Maskierung" zu verweisen, das verwandt ist mit dem Mach-Effekt, aber trotzdem davon abweicht. Es wurde festgestellt, dass die Helligkeitsänderungsschwelle (siehe oben) empfindlich auf die Anwesenheit eines in der Nähe auftretenden Helligkeitssprungs reagiert. Anders gesagt ist der Schwellwert höher als er wäre, wenn der Helligkeitssprung nicht vorhanden wäre. Deshalb sagt man, der Sprung maskiert kleine Helligkeitsunterschiede in seiner Umgebung. Ein weiteres wichtiges Merkmal dieses Maskierungseffekts liegt darin, dass er eine Funktion des Gradienten der Hellikeitsänderung ist, gegenüber der er gemessen wird (in einem typischen Bild ist er deshalb abhängig vom anvisierten Detail). Dieser Umstand wurde dazu benutzt, um Maskierungsfunktionen auf der Basis von gewichteten Ableitungen der Helligkeitsverteilung innerhalb eines einige Pixel umfassenden Bereichs zu definieren. Diese können dazu verwendet werden, den Quantisierungsprozess von Codiersystemen mit Vorhersage zu optimieren. Dies ist ein erfolgreiches Beispiel für die Einbeziehung von Eigenschaften des HVS in Bildcodieralgorithmen, da der Quantisierungsfehler jetzt in direkter Beziehung zum dargestellten Helligkeitswert steht. Bevor ich näher auf Modelle der menschlichen visuellen Wahrnehmung eingehe, muss noch ein Umstand erläutert werden, der unabhängig von den Prozessen auf der Netzhaut ist. Und zwar handelt es sich um die Arbeitsweise der reinen optischen Abbildung durch Pupille und Linse. Messungen der Lichtverteilung auf der Netzhaut nach der Abbildung des Auges haben folgende gauss`sche Verteilungsfunktion ergeben:
 ,
die den 3-dB Punkt bei Die wichtigsten Faktoren des menschlichen visuellen Wahrnehmungsvorgangs müssen jetzt in einem Gesamtmodell vereinigt werden, das anschliessend zum Beispiel dazu verwendet werden kann, Bildkomprimierungsverfahren effizienter zu gestalten oder - wie in unserem Fall - um die subjektiven Tests zur Beurteilung der Bildqualität zu ersetzen. Modellierung des HVSDie wichtigsten Merkmale des HVS, die im Modell berücksichtigt werden müssen sind:
Es stellt sich ausserdem die Frage, ob ein Erkennungsmechanismus an den Ausgang der vorhergehenden Verarbeitungsstufen gekoppelt werden soll, der feststellen soll, ob der empfangene Stimulus wahrgenommen wurde oder nicht. Ein Modell, das den oben genannten Ansprüchen genügt, ist in Bild 5.7 dargestellt. Die optionale Wahrnehmungsdetektion könnte wie darunter gezeigt realisiert werden.
 Da es sehr viele Modelle gibt, die dieser allgemeinen Definition entsprechen und entsprechend viele Anwendungsgebiete, für die der grösste Teil spezialisiert ist, beschränke ich mich auf Modelle , die
Innerhalb dieses vorgegebenen Rahmens werden demnach zwei Eingangsbilder I0 (Original) und I1 (verändert) vom Berechnungsmodell P bewertet und danach wird ein Abstand Q nach der Integrationsregel" Q(P(I0),P(I1)) ermittelt:
Diese Gleichung errechnet den euklidischen Abstand für E = 2, approximiert die Aufaddierung der Wahrscheinlichkeiten für E = 4 und findet die maximale absolute Differenz für Als Übersicht werden in Tabelle 2 einige Verfahren zur Bildqualitätsbeurteilung vorgestellt, die auf oben beschriebenem Modell basieren. Bei genauer Betrachtung stellt man fest, dass alle Verfahren auch als vereinfachtes Lubin-Modell bezeichnet werden könnten. Die Abkürzungen haben folgende Bedeutung:
 |
der Umgebungsbeleuchtung ist. Das visuelle System reagiert folglich, zumindest an oder in der Nähe der Schwelle, auf geringfügige Veränderungen, was bedeutet, dass die Beziehung zwischen der Reaktion und der Anregung logarithmisch verläuft, und dass die Wahrnehmung der Helligkeit vom Verhältnis der Objekt- zur Umgebungsbeleuchtungen viel mehr abhängt als vom Absolutwert der ersteren. Das bedeutet, dass eine Störung einer gegebenen Grösse (z. B. Rauschen) innerhalb dunkler Bildanteile viel stärker bemerkt wird als anderswo.Tatsächlich wird dieser Effekt aber durch die Nichtlinearität des verwendeten Displays verändert zu
typischerweise den Wert 2.5 darstellt, wodurch die logarithmische Funktionsweise beim Amplitudengang des Auges rückgängig gemacht wird [24]. Somit wird die Reaktion insgesamt gesehen nahezu zu einer linearen Funktion des durch das System hervorgerufenen elektrischen Störsignals (analoges oder Quantisierungsrauschen). In Wirklichkeit wird durch die immer vorhandene Umgebungsbeleuchtung in der Nähe des Displays sogar allfällige Verschlechterungen, (z. B. hervorgerufen durch Rauschen) in dunklen Flächen weniger stark wahrgenommen als in helleren Bildanteilen. Es besteht somit eine viel komplexere Beziehung zwischen der Wahrnehmung direkt an der visuellen Helligkeitunterscheidbarkeitsschwelle, in Bereichen in der Nähe der Schwelle und in entfernteren Bereichen, als man auf den ersten Blick vermuten könnte [26].
wird in Winkelminuten gemessen und 
ist 0,7 für einen Pupillendurchmesser von 3 mm. Die Fouriertransformierte von 
ergibt die Übertragungsfunktion 
Schwingungen / Grad hat. Das bedeutet, dass die einfallende visuelle Information durch das optische System tiefpassgefiltert wird, bevor überhaupt retinale und neuronale Verarbeitungen beginnen. Insbesondere tritt diese Filterung vor der logarithmischen Nichtlinearität auf, was auch einen Einfluss auf das entsprechende räumliche Arbeitsmodell des HVS (siehe unten) hat.
.
